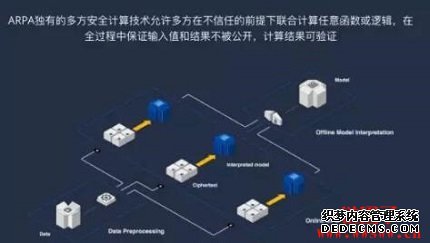
多方计较（Multi-party computation，MPC）是一种暗码学技能，它可以让多个参加方在不泄露各自的数据的环境下，配合计较一个函数的功效。这种技能可以应用于许多场景，譬喻隐私掩护的拍卖、投票、呆板进修、基因阐明等。本文将先容多方计较的根基观念、安详模子、协议结构和实际应用。

多方计较的根基观念是，假设有n个参加方，每个参加方有一个私密的输入x_i，他们想要计较一个民众的函数f(x_1,x_2,…,x_n)=(y_1,y_2,…,y_n)，个中y_i是第i个参加方的输出。多方计较的方针是设计一个协议，使得每个参加方可以获得本身的输出y_i，而不泄露本身可能其他参加方的输入x_i。换句话说，多方计较要担保以下两本性质：

• 正确性：每个参加方获得的输出y_i是函数f在所有参加方的输入上的正确功效。
• 隐私性：每个参加方除了获得本身的输出y_i之外，不能得到其他任何干于其他参加方输入x_j的信息。

多方计较的安详模子是指，在协议执行进程中，大概存在一些不厚道的参加方，他们大概会试图粉碎协议的正确性可能隐私性。按照不厚道参加方的行为和本领，可以界说差异的安详模子。常见的安详模子有以下几种：

• 半厚道模子：在这个模子中，假设所有的参加方城市凭据协议划定正确地执行协议，，可是他们会实验从协议中得到特另外信息。这个模子相当于假设所有的参加方都是“好奇”的，但不会“作弊”的。
• 恶意模子：在这个模子中，假设有一部门参加方大概会任意地违反协议划定，好比发送错误可能伪造的信息，拒绝发送信息，可能勾串其他恶意参加方。这个模子相当于假设所有的参加方都是“敌对”的，而且会尽大概地“作弊”。
• 静态/自适应模子：在这两个模子中，假设有一个外部对手可以节制一部门参加方，而且可以看到他们节制的参加方的所有信息。区别在于，在静态模子中，对手必需在协议开始之前就确定要节制哪些参加方；而在自适应模子中，对手可以在协议执行进程中动态地选择要节制哪些参加方。

多方计较的协议结构是指，如何操作暗码学东西和技能来设计满意特定安详模子要求的多方计较协议。按照协议涉及的参加方数量和函数范例，可以将协议分为以下几类：

• 两方计较：这是最简朴的景象，只有两个参加方想要计较一个函数。这种景象下有许多经典的协议和问题，譬喻姚氏百万大亨问题、姚氏垃圾邮件过滤器、姚氏夹杂电路等。
• 多项式函数计较：这是一类非凡的函数范例，即函数可以暗示为多项式形式。这种景象下有许多基于奥秘分享的协议，譬喻Shamir奥秘分享、Ben-Or等人的协议、Beaver等人的协议等。
• 一般函数计较：这是最一般的景象，即函数可以是任意的可计较函数。这种景象下有许多基于电路暗示的协议，譬喻Goldreich等人的协议、Lindell和Pinkas的协议、Ben-Sasson等人的协议等。

多方计较的实际应用是指，如何将多方计较技能应用于办理现实世界中的问题。由于多方计较可以掩护数据隐私，因此它在许多规模都有遍及的应用代价，譬喻：

• 隐私掩护的拍卖：多方计较可以让多个买家和卖家在不泄露本身的出价和需求的环境下，举办公正和有效的拍卖。譬喻，Tezori和Santis等人提出了一个基于SMPC的隐私掩护的双边拍卖协议。
• 隐私掩护的投票：多方计较可以让多个选民和候选人在不泄露本身的选票和得票数的环境下，举办安详和正确的投票。譬喻，Cramer等人提出了一个基于SMPC的隐私掩护的电子投票协议。
• 隐私掩护的呆板进修：多方计较可以让多个数据拥有者和模子练习者在不泄露本身的数据和模子参数的环境下，举办高效和精确的呆板进修。譬喻，Mohassel和Zhang提出了一个基于SMPC的隐私掩护的神经网络练习协议。
• 隐私掩护的基因阐明：多方计较可以让多个基因数据拥有者和阐明者在不泄露本身的基因数据和阐明功效的环境下，举办巨大和敏感的基因阐明。譬喻，Cho等人提出了一个基于SMPC的隐私掩护的基因组关联阐明协议。

总之，多方计较是一种掩护数据隐私的暗码学技能，它可以让多个参加方在不泄露各自的数据的环境下，配合计较一个函数的功效。

郑重声明：本文版权归原作者所有，转载文章仅为传播更多信息之目的，如作者信息标记有误，请第一时间联系我们修改或删除，多谢。